Cайт "Забытая русская история" 2018 год
Математическая модель Великого потопа
или Модель Каспийского озера (Цепи озер) во времена допотопные
Маршрут приключения Шумерского царя Гильгамеша
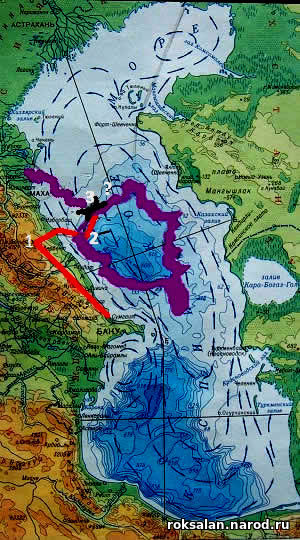

Маршрут приключения Шумерского царя Гильгамеша
Схема дна ГЛУБОКОГО МОРЯ древних - усыхающей Дербентской впадины
Разливы Хвалынского моря
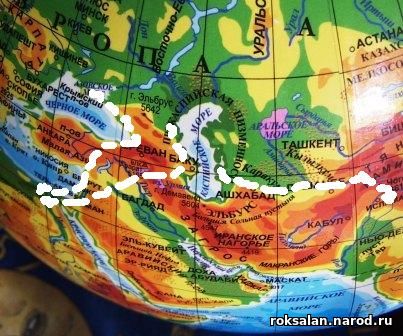
Маршруты исходов атлантов от Понта и Каспия в Египет и в Индию и Пакистан
Математическая модель Великого потопа или Модель Каспийского озера (Цепи озер)
Времена допотопные (на электронных таблицах)Описание модели.
Предлагаю рассмотреть математическую
модель изменения во времени соотношения водной
поверхности южных морей Русской равнины и
затапливаемых ими прилегающих территорий суши.
Район рассмотрения удален от Мирового океана,
отгорожен от него горными преградами, а поэтому в
прошлом условно может считаться изолированным и
связанным с Мировым океаном только через
атмосферу планеты. В связи с циклическим
изменением количества осадков выпадающих над
сушей, а также с изменением испаряемости с
водной поверхности морей, будем полагать, что
огромная протяженность рек будет сглаживать
неравномерность распределения осадков по
пересекаемой ими территории суши, также как
большая протяженность морей поперек широтных
климатических поясов будет выравнивать
неодинаковую испаряемость с разных районов моря.
Будем учитывать, что моря юга Русской равнины
расположены примерно в одном климатическом
поясе. А кроме того, рассмотрение параметров
водоносности рек в целом за год позволят не
рассматривать сезонные колебания. С учетом этих
обстоятельств будем рассматривать многолетнюю
устойчивость водоемов и их природных
объединений. Предполагаем, что если водоем не
успевает испарять приносимую ему реками воду, то
он начинает повышать свой уровень и затоплять
берега, увеличивая свою площадь. А если воды
испаряется больше, чем приносят реки, то водоем
усыхает, уровень его понижается, а площадь
сокращается. И в том, и в этом случае водоем можно
будет считать неустойчивым и не имеющим права
долговременного существования в отведенных ему
природой пределах.
Испытание модели (контрольные проверки)
Современное Каспийское море.
Баланс современного Каспия выполняется
моделью практически идеально в пределах точности
исходных данных модели. Испаряемость увеличена
всего на 2,5 процента.
Современное Черное море.
Черноморский бассейн современной площади
сможет существовать, если испаряемость его
поверхности будет в два раза меньше, чем
испаряемость на Каспии (49,6 процентов). Общение
моря с океаном через проливы вводят
саморегуляцию уровня моря. При повышении
испаряемости усиливается приток соленой воды, при
понижении испаряемости усиливается слив воды
через Боспор. Умозрительная оценка климатических
условий Черного и Каспийского морей согласуется с
полученной оценкой испаряемости на Черном море в
два раза меньшей, чем на Каспии. Использование модели для проверки
гипотез
Замкнутый Азово-Черноморский бассейн.
Древнее состояние морей на основе моей
реконструкции Меотиды и реконструкции карт
Птолемея для Понта таково. Меотида по площади в
семь раз меньше современного Азовского моря (14%). Понт на 30% меньше Черного моря за счет
мелководья у берегов. Водоносность Танаиса вдвое
меньше чем у Дона, за счет Сарпинского рукава в Каспий.
Замкнутый Черноморско-Азовский бассейн
даже современной площади будет переполняться и
должен будет сбрасывать излишек воды в Каспий в
объеме стоков большой реки, такой, как Дунай (186
куб. км). При меньшей площади морей в древности
(14 процентов для площади Меотиды от площади
современного Азовского моря и 70 процентов для
Понта от площади современного Черного моря) в
Каспий сбрасывалось воды еще больше (240 куб км).
Хвалынское море.
Море было подпружено с юга
Предкавказскими (Керавнийскими горами). Климат
был более жаркий, чем современный. Геологи
существование Хвалынского моря относят к
Московско-Валдайскому межледниковью. В море
впадали все реки Северного Каспия. Из
Черноморско-Азовского бассейна по рукаву Дона и
(или) по Кума–Маныческому прогибу поступает
избыток воды по объему примерно равный стоку
современного Днепра. Равновесие моделью
достигнуто при площади Хвалынского моря почти в
четыре раза превышающего (3,85) площадь
современного северного Каспия. При таком
соотношении Хвалынское море должно было
занимать всю Прикаспийскую низменность
(темнозеленый цвет на карте) и Северный Каспий.
Прикаспийская низменность – это видимо след от
Хвалынского моря
Атлантическое и Красное моря
Без притока северных рек это усыхающие
водоемы на дне глубоководных чаш. По площади
они равняются 43 процентам Среднего и Южного Каспия.
Атлантическое и Красное моря, и озеро Гелиоса
Система водоемов у Атлантиды: озеро
Гелиоса, соединенное проливом у Геракловых
столпов с Атлантическим и Красным морями античности.
Озеро Гелиоса по площади равнялось
Северному Каспию. Испаряемость моря была
принята повышенной в 1,5 раза или мною вводился
феномен Геракловых столпов – река в небеса стоком
166 куб. км. Для сравнения, Волга имеет сток 256
куб. км. После гибели Атлантиды баланс получился за
счет расширения моря. Озеро Гелиоса по-прежнему
равняется площади Северного Каспия, но море
затопило равнину атлантов. Испаряемость была
принята на 11 процентов больше, чем современная и
исчез феномен Геракловых столпов – река в небеса.
Атлантическое и Красное моря и озеро
Гелиоса без притока от Черного моря и без
Сарпинского рукава Дона.
Исходные данные приведены в последующей таблице и в пояснениях.
Формулы модели записаны простым текстом в
правой нижней части таблицы со ссылками на
адреса столбцов (слева-направо): A,B,C,D и
номерами строк (сверху-вниз). Адреса ячеек при
расчете определялись, например, так: годовой сток
Волги в 256 кубических километров расположен в
четвертом (D) столбце, четвертой (4) строки
таблицы. Следовательно, адрес ячейки таблицы с
годовым стоком Волги будет таким: D4. В формулах
баланса этот адрес присутствует при суммировании
(СУММ() или SUM()) стоков рек бассейна Каспия.
Баланс Черноморского бассейна SUM(B4:B12)+B30+B29-D28*B21*0,496-B13
Баланс замкнутого Черного моря современной площади
SUM(B4:B12)+B30+B29-D28*B21*0,835-B12-B7/2
Баланс Понта с Меотидой (0.7 и 0.14) SUM(B4:B11)+B30+(B19*0,14+B20*0,7)*(B29/B21-B28*0,496)-B7/2
Баланс Каспийского бассейна SUM(D4:D14)+D29+D30-D20*D28*1,025-D17-D6-D12
Баланс Хвалынского моря SUM(D4:D7)+D29/D20*B33*3,85+D30/4+B36-D28*B33*1,5*3,85
Баланс Атланто-Красного моря SUM(D8:D13)+D29/D20*(D22+D23)*0,34+D30*1/2-(D22+D23)*D28*0,34
Баланс Атланто-Красного моря с оз.Гелиоса SUM(D4:D14)+B36+D29/D20*(B33*1,01+D23+D22)+D30-(B33*1,01+D23+D22)*D28*1,0
Баланс Каспия после катастрофы с Атлантидой SUM(D4:D14)+D29/D20*(D21+D22+D23+B33*1)+D30-D6-D17-(D21+D22+D23+B33*1)*D28*1,105
Модель прошла «обкатку» на моем сайте в
интернете.
Читатели, познакомившись с нею, живо
интересовались подобной же моделью для региона
Средиземноморья.
На что я им отвечал, что логично
внутренних морей Атлантического океана от
Гибралтара через Средиземное, Черное, Азовское
моря
через реки и проливы до самого Южного
Каспия. Моя модель Потопа и сценарий к нему
предусматривают только половину из этой цепочки
(от Босфора Фракийского). Со временем постараюсь
собрать информацию и для Средиземного моря.
Модель моя позволит рассчитать его площадь и
уровень, а тогда можно будет порассуждать о
масштабах наводнения и о мощности потока из
океана после землетрясения или прорыва океана в
районе Гибралтара, если Средиземное море
окажется усыхающим. Для книги подготовлена
такая модель для Черного и Каспийского морей.
Результаты получаются великолепные...
Модель готова к применению, достаточно
лишь перенести информацию в электронную
таблицу Excell и ввести по правилам формулы,
которые внизу таблицы в соответствующих
надписанных ячейках.
А сейчас приведу информацию к
размышлению по истории региона и
землетрясениям, преобразующим его географию.
САЙТ "ЗРИ" ПРЕДСТАВЛЯЕТ
ЧУДО Каменного века! Все дно Каспия "украшено" разломами различной по давности веками происхождения. Отмечены и берега Глубокого моря. Море-озеро "отметило" и борта впадины своей "жизнедеятельности". Разрезы впадин тоже оставили свой "автограф". Читаются на морском берегу и озера возле канала и архонства Гадирии и древний берег моря-озера.
Типовое обращение
Я, Владимир Амельченко [Roksalan] (10.03.2018 19:57)
Привет! Хочу зарегистрироваться на сайте,
мой псевдоним: roksalan
мой e-майл : vamelchenko@gmail.com телефон: +9181688155
Я - весь ВНИМАНИЕ
Нижний колонтитул © 1997—2018
Cайт "Забытая русская история" 2018 год
Математическая модель Великого потопа
или Модель Каспийского озера (Цепи озер) во времена допотопные
Маршрут приключения Шумерского царя Гильгамеша



| Маршрут приключения Шумерского царя Гильгамеша | Схема дна ГЛУБОКОГО МОРЯ древних - усыхающей Дербентской впадины | Разливы Хвалынского моря |
Маршруты исходов атлантов от Понта и Каспия в Египет и в Индию и Пакистан
Математическая модель Великого потопа или Модель Каспийского озера (Цепи озер) |
Времена допотопные (на электронных таблицах)Описание модели. |
Предлагаю рассмотреть математическую модель изменения во времени соотношения водной поверхности южных морей Русской равнины и затапливаемых ими прилегающих территорий суши. Район рассмотрения удален от Мирового океана, отгорожен от него горными преградами, а поэтому в прошлом условно может считаться изолированным и связанным с Мировым океаном только через атмосферу планеты. В связи с циклическим изменением количества осадков выпадающих над сушей, а также с изменением испаряемости с водной поверхности морей, будем полагать, что огромная протяженность рек будет сглаживать неравномерность распределения осадков по пересекаемой ими территории суши, также как большая протяженность морей поперек широтных климатических поясов будет выравнивать неодинаковую испаряемость с разных районов моря. Будем учитывать, что моря юга Русской равнины расположены примерно в одном климатическом поясе. А кроме того, рассмотрение параметров водоносности рек в целом за год позволят не рассматривать сезонные колебания. С учетом этих обстоятельств будем рассматривать многолетнюю устойчивость водоемов и их природных объединений. Предполагаем, что если водоем не успевает испарять приносимую ему реками воду, то он начинает повышать свой уровень и затоплять берега, увеличивая свою площадь. А если воды испаряется больше, чем приносят реки, то водоем усыхает, уровень его понижается, а площадь сокращается. И в том, и в этом случае водоем можно будет считать неустойчивым и не имеющим права долговременного существования в отведенных ему природой пределах.
Испытание модели (контрольные проверки)
Современное Каспийское море.
Баланс современного Каспия выполняется моделью практически идеально в пределах точности исходных данных модели. Испаряемость увеличена всего на 2,5 процента.
Современное Черное море.
Черноморский бассейн современной площади сможет существовать, если испаряемость его поверхности будет в два раза меньше, чем испаряемость на Каспии (49,6 процентов). Общение моря с океаном через проливы вводят саморегуляцию уровня моря. При повышении испаряемости усиливается приток соленой воды, при понижении испаряемости усиливается слив воды через Боспор. Умозрительная оценка климатических условий Черного и Каспийского морей согласуется с полученной оценкой испаряемости на Черном море в два раза меньшей, чем на Каспии. Использование модели для проверки гипотез
Замкнутый Азово-Черноморский бассейн.
Древнее состояние морей на основе моей реконструкции Меотиды и реконструкции карт Птолемея для Понта таково. Меотида по площади в семь раз меньше современного Азовского моря (14%). Понт на 30% меньше Черного моря за счет мелководья у берегов. Водоносность Танаиса вдвое меньше чем у Дона, за счет Сарпинского рукава в Каспий.
Замкнутый Черноморско-Азовский бассейн даже современной площади будет переполняться и должен будет сбрасывать излишек воды в Каспий в объеме стоков большой реки, такой, как Дунай (186 куб. км). При меньшей площади морей в древности (14 процентов для площади Меотиды от площади современного Азовского моря и 70 процентов для Понта от площади современного Черного моря) в Каспий сбрасывалось воды еще больше (240 куб км).
Хвалынское море.
Море было подпружено с юга
Предкавказскими (Керавнийскими горами). Климат
был более жаркий, чем современный. Геологи
существование Хвалынского моря относят к
Московско-Валдайскому межледниковью. В море
впадали все реки Северного Каспия. Из
Черноморско-Азовского бассейна по рукаву Дона и
(или) по Кума–Маныческому прогибу поступает
избыток воды по объему примерно равный стоку
современного Днепра. Равновесие моделью
достигнуто при площади Хвалынского моря почти в
четыре раза превышающего (3,85) площадь
современного северного Каспия. При таком
соотношении Хвалынское море должно было
занимать всю Прикаспийскую низменность
(темнозеленый цвет на карте) и Северный Каспий.
Прикаспийская низменность – это видимо след от
Хвалынского моря
Атлантическое и Красное моря
Без притока северных рек это усыхающие
водоемы на дне глубоководных чаш. По площади
они равняются 43 процентам Среднего и Южного Каспия.
Атлантическое и Красное моря, и озеро Гелиоса
Система водоемов у Атлантиды: озеро
Гелиоса, соединенное проливом у Геракловых
столпов с Атлантическим и Красным морями античности.
Озеро Гелиоса по площади равнялось
Северному Каспию. Испаряемость моря была
принята повышенной в 1,5 раза или мною вводился
феномен Геракловых столпов – река в небеса стоком
166 куб. км. Для сравнения, Волга имеет сток 256
куб. км. После гибели Атлантиды баланс получился за
счет расширения моря. Озеро Гелиоса по-прежнему
равняется площади Северного Каспия, но море
затопило равнину атлантов. Испаряемость была
принята на 11 процентов больше, чем современная и
исчез феномен Геракловых столпов – река в небеса.
Атлантическое и Красное моря и озеро
Гелиоса без притока от Черного моря и без
Сарпинского рукава Дона.
Исходные данные приведены в последующей таблице и в пояснениях.
Формулы модели записаны простым текстом в
правой нижней части таблицы со ссылками на
адреса столбцов (слева-направо): A,B,C,D и
номерами строк (сверху-вниз). Адреса ячеек при
расчете определялись, например, так: годовой сток
Волги в 256 кубических километров расположен в
четвертом (D) столбце, четвертой (4) строки
таблицы. Следовательно, адрес ячейки таблицы с
годовым стоком Волги будет таким: D4. В формулах
баланса этот адрес присутствует при суммировании
(СУММ() или SUM()) стоков рек бассейна Каспия.
Атлантическое и Красное моря, и озеро Гелиоса
Система водоемов у Атлантиды: озеро Гелиоса, соединенное проливом у Геракловых столпов с Атлантическим и Красным морями античности.
Озеро Гелиоса по площади равнялось Северному Каспию. Испаряемость моря была принята повышенной в 1,5 раза или мною вводился феномен Геракловых столпов – река в небеса стоком 166 куб. км. Для сравнения, Волга имеет сток 256 куб. км. После гибели Атлантиды баланс получился за счет расширения моря. Озеро Гелиоса по-прежнему равняется площади Северного Каспия, но море затопило равнину атлантов. Испаряемость была принята на 11 процентов больше, чем современная и исчез феномен Геракловых столпов – река в небеса. Атлантическое и Красное моря и озеро Гелиоса без притока от Черного моря и без Сарпинского рукава Дона.
Исходные данные приведены в последующей таблице и в пояснениях. Формулы модели записаны простым текстом в правой нижней части таблицы со ссылками на адреса столбцов (слева-направо): A,B,C,D и номерами строк (сверху-вниз). Адреса ячеек при расчете определялись, например, так: годовой сток Волги в 256 кубических километров расположен в четвертом (D) столбце, четвертой (4) строки таблицы. Следовательно, адрес ячейки таблицы с годовым стоком Волги будет таким: D4. В формулах баланса этот адрес присутствует при суммировании (СУММ() или SUM()) стоков рек бассейна Каспия.
Баланс Черноморского бассейна SUM(B4:B12)+B30+B29-D28*B21*0,496-B13
Баланс замкнутого Черного моря современной площади
SUM(B4:B12)+B30+B29-D28*B21*0,835-B12-B7/2
Баланс Понта с Меотидой (0.7 и 0.14) SUM(B4:B11)+B30+(B19*0,14+B20*0,7)*(B29/B21-B28*0,496)-B7/2
Баланс Хвалынского моря SUM(D4:D7)+D29/D20*B33*3,85+D30/4+B36-D28*B33*1,5*3,85
Баланс Атланто-Красного моря SUM(D8:D13)+D29/D20*(D22+D23)*0,34+D30*1/2-(D22+D23)*D28*0,34
Баланс Атланто-Красного моря с оз.Гелиоса SUM(D4:D14)+B36+D29/D20*(B33*1,01+D23+D22)+D30-(B33*1,01+D23+D22)*D28*1,0
Баланс Каспия после катастрофы с Атлантидой SUM(D4:D14)+D29/D20*(D21+D22+D23+B33*1)+D30-D6-D17-(D21+D22+D23+B33*1)*D28*1,105
Модель прошла «обкатку» на моем сайте в
интернете.
Читатели, познакомившись с нею, живо
интересовались подобной же моделью для региона
Средиземноморья.
На что я им отвечал, что логично
внутренних морей Атлантического океана от
Гибралтара через Средиземное, Черное, Азовское
моря
через реки и проливы до самого Южного
Каспия. Моя модель Потопа и сценарий к нему
предусматривают только половину из этой цепочки
(от Босфора Фракийского). Со временем постараюсь
собрать информацию и для Средиземного моря.
Модель моя позволит рассчитать его площадь и
уровень, а тогда можно будет порассуждать о
масштабах наводнения и о мощности потока из
океана после землетрясения или прорыва океана в
районе Гибралтара, если Средиземное море
окажется усыхающим. Для книги подготовлена
такая модель для Черного и Каспийского морей.
Результаты получаются великолепные...
Модель готова к применению, достаточно
лишь перенести информацию в электронную
таблицу Excell и ввести по правилам формулы,
которые внизу таблицы в соответствующих
надписанных ячейках.
А сейчас приведу информацию к
размышлению по истории региона и
землетрясениям, преобразующим его географию.
САЙТ "ЗРИ" ПРЕДСТАВЛЯЕТ